géométrie fractale...  

Benoît Mandelbrot

Les fractales sont considérées comme des figures irrégulières, ramifiées, et arborescentes dont la structure fait souvent intervenir la reproduction de motifs par fractionnement.

En 1970, Benoît Mandelbrot permit à ces figures de devenir l'objet d'une branche mathématique à part entière. "Les nuages ne sont pas des sphères!" s'amusait à dire ce mathématicien français.

Observons à titre d'exemple une simple pelote de laine. De loin elle nous apparaîtra comme un point, de plus près il s'agira globalement d'une sphère. Observée d'encore plus près, elle sera réduite à un fil, et ainsi de suite... Cette même pelote pourra donc être perçue différemment, selon l'échelle à laquelle on l'observera, offrant ainsi une série de nouvelles perceptions... Phénomène que l'on peut retrouver dans tout système de nature fractale.

La courbe de Koch

"La courbe de Koch", du nom du mathématicien suédois qui l'a inventée, rappelle la structure d'un flocon de neige. Pour tracer cette courbe infinie, il suffit de reproduire un grand nombre de fois le motif de départ, à savoir un triangle équilatéral.

Cette courbe devient alors infiniment longue, "aussi longue qu'une droite euclidienne qui s'étendrait jusqu'aux limites d'un univers sans borne"... Ce résultat paradoxal, d'une longueur infinie contenue dans un espace fini, perturba de nombreux mathématiciens.

Le triangle de Sierpinski

Le triangle de Sierpinski est obtenu en partant d'un triangle équilatéral. On prend les milieux de chacun de ses côtés, on relie les points, et on enlève le triangle équilatéral obtenu. On obtient alors 3 nouveaux triangles équilatéraux. On peut ensuite réitérer l'opération à chaque triangle... On obtient alors 9, 27, 81,... autres triangles fait de nouveaux petits détails.

l'éponge de Menger

Construction : Si l’on partage chacune des arêtes en 3 parties égales, chaque face sera formée d’un damier de neuf carrés. Commençons par vider celui du milieu. En ajoutant les parois de cette partie évidée, la superficie de la structure est alors plus grande que celle du cube d’origine. De ce fait, nous augmentons la surface sans en faire varier le volume.

Chacun des 8 carrés restants est désormais divisé en un minuscule damier de 9, dont la figure centrale est à nouveau évidée... et ainsi de suite, jusqu’à atteindre des portions microscopiques. A force de creuser dans le volume de départ, la surface ne cesse d’augmenter, certes d’une quantité de plus en plus petite, mais... sans aucune limite. Au final, on aura une dentelle tridimensionnelle qui ne débordera pas du cube d’origine.

la nature fractale de l'univers

La récurrence d’un motif au sein d'un autre motif se retrouve dans de nombreux phénomènes naturels. Elle peut être perçue dans les nuages, les cristaux, les chaînes de montagnes, les côtes maritimes, les arbres... On la discerne également dans la forme des galaxies ou encore dans celle des nuages interstellaires...

les côtes rocheuses

Combien mesure la côte de la Bretagne ? - Cette question posée au début des années 60 par le britannique L.F.Richardson n'est pas aussi simple qu'elle y paraît. Les littoraux de la Bretagne sont en effet très irréguliers, ils sont pleins de criques, de renfoncements, et de rivages rocheux.

Prenons une image satellite de la Bretagne et mesurerons la longueur de sa côte. Pour ce faire, nous utiliserons un compas d'une ouverture fixée, notée x. En comptant le nombre d'ouvertures obtenu après avoir parcouru la côte, nous obtiendrons alors une certaine longueur.

Maintenant, zoomons un peu plus vers ce littoral breton, où nous n'allons par tarder à découvrir de nouvelles formes, de nouveaux renfoncements...

Si jamais on réitère l'expérience du compas, avec cette fois-ci une ouverture plus petite, on remarquera que la longueur de la côte devient plus importante, et qu'elle ne cesse d'augmenter...  Comme si finalement, nous plongions dans un puit sans fond aux formes répétitives et infinies...

L'estimation de cette mesure dépend donc de l'instrument utilisé, de la finesse de l'observation, et en définitive, de l'observateur lui-même. Tout n'est qu'une question d'échelle. La mesure et le mesureur participent activement du phénomène observé et le modifie...

le règne végétal

La nature cache en elle les plus belles représentations géométriques qui d'une certaine manière se veulent aussi inspirées que variées. Pour les apercevoir, il suffit simplement d'ouvrir les yeux, et de regarder autour de nous... Un certain nombre de ces formes fractales se retrouvent en effet dans le règne végétal. C’est le cas du chou-fleur, du chou romanesco, des  fougères, des racines, de la forme des feuilles, ou encore de leurs nervures...

Un arbre par exemple est considéré comme une figure fractale, dans le sens où ses branches seront perçues comme de véritables arbres en miniature.

Même si l’étude des formes fractales est assez récente, il semblerait que les espèces végétales ont développé cette structure afin d'augmenter leur "surface" d’échange avec le milieu extérieur. Cette nécessité ce serait alors dessinée, manifestée dans le simple but de favoriser leur évolution.

En se penchant sur le caractère fractal de la nature, les mathématiciens montrèrent que l'on pouvait générer toute forme, aussi complexe soit-elle.

Pour ce faire, il suffisait  d'utiliser un ensemble de fonctions simples, et les réitérées un grand nombre de fois. Dès lors et selon ce principe, ils pouvaient simuler la croissance de nombreux végétaux, et obtenir des images très réalistes.

le corps humain

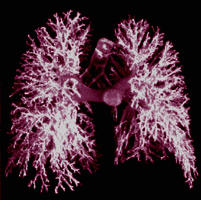
Le corps humain regorge d'une multitude de structures fractales. C’est le cas des voies respiratoires et de sa prodigieuse ramification, de certaines parties du coeur, de nos vaisseaux et son vaste réseau sanguin... Toutes ces structures ont été élaborées lors du développement de l'embryon qui a fait intervenir un caractère chaotique et déterministe à sa propre évolution.

"Certains biologistes commencèrent à découvrir qu'une organisation fractale contrôlait les structures à tous les niveaux du corps humain: Des impulsions aux muscles cardiaques, tout cela se révéla fractal. Un labyrinthe de bifurcations autosimilaires sur des échelles de plus en plus petites." J. Gleick

visions artistiques

Quand les mathématiques riment avec beauté...

Découverts par les mathématiciens français Gaston Julia et Pierre Fatou, ces ensembles d'objets mathématiques ne tardèrent pas à donner naissance à une multitude de formes fractales qui se voulaient aussi complexes qu'infinies...

La beauté insoupçonnée de l’ensemble de Mandelbrot, ou encore celle découverte dans les ensembles de Julia  (cf image ci-contre) ont par la suite laissé place à une toute nouvelle forme d'art.

A l'heure où l'ère numérique entre ouvre ses portes, on peut alors se demander si l'art fractal ne tendra pas à se développer - permettant ainsi de "créer" voire de "simuler", via une simple formule mathématique, des formes abstraites, esthétiques, et quasi réelles de l'Univers...

l'univers...

«  Voir un univers dans un grain de sable. Et un paradis dans une fleur sauvage, Tenir l'infini dans la paume de la main, Et l'éternité dans une heure.» William Blake

Selon le physicien David Bohm chaque région de l'espace-temps, si petite soit-elle, contiendrait une information sur l'ordre impliqué dans des dimensions beaucoup plus grandes. Aux vues de nos observations, l'Univers semblerait en effet contenir toute une famille, une hiérarchie de formes fractales, comme si ce grand tout unique avait la possibilité de se déployer à l'infini...

Plonger dans le mystérieux objet de Hoag ou encore au creux de ces galaxies nous révèlera par exemple une multitude de nouveaux mondes. Toutes ces structures (tels les planètes, les étoiles, les galaxies, les amas, les trous noirs...) sont également entraînées dans un mouvement perpétuel et interactif. Cet immense ballet cosmique se compose alors de mouvements de révolution, de rotation, d'éloignement, et d'approche.

Si l'Univers possède un comportement fractal, au sein de tous ces mondes qui s'emboîtent les uns dans les autres, on peut imaginer que ce qui est vrai pour l'Un, l'est aussi pour tous ses constituants (Galaxie, Soleil, Terre, Lune...) Ce qui renforcerait l'idée que les lois régissant l'évolution de l'Univers, et ce à toutes échelles, ne sont ni aléatoires ou absurdes. Elles seraient au contraire le fruit d'un processus d'organisation et d'interactions très précises, comme si finalement tout avait un sens, telle une structure unifiante qui s'étendrait dans l'infini... (cf : Voyage vers l'infiniment petit...)